Articles about pieces of technology generally come in three phases:
- The first phase comes from the press, who’ve either had access to early versions of the device or are there at the launch event. They have stuff pre-written, primed and ready to go so that as soon as the product is officially announced, people will be able to find something as soon as they hit Google.
- The second phase comes from the first people who are actually able to buy the product, generally a few weeks later. These are naturally accompanied by the obligatory unboxing videos (a hilariously fascinating genre of content if ever there was one) and generally give first impressions of each device (they can’t give much else because, you know, they just opened the thing 5 minutes ago).
- The third phase are the “long term” reviews, maybe a month or two later. There are fewer of these because the initial excitement has died down, but people are actually interested in giving their thoughts now that they’ve gotten used to how the device works and can give a more measured explanation of its pros and cons.
And then there are articles like this one, which… well, the iPad Pro was released almost a year ago now. It’s been so long since I first got this device that another iPad Pro has already been released in the intervening time. So why do I think it’s still relevant to write this thing?
Basically, it’s because I’m still getting questions about my iPad Pro wherever I take it. It’s my preferred device for taking notes – so I lug it around with me to any conferences I attend – and pretty much every time I get it out, someone nearby will say, “what is that?” And when I explain that it’s an iPad, I’m almost universally met with surprise. So I guess, despite this tablet’s age, there are still plenty of people out there who don’t know much about it. So hopefully this will give you a bit of a better idea.
This is not a product review. It’s more of a reflection on my specific experience with this pair of devices. But in some ways, it’s the review I couldn’t find. Before I got my hands on an iPad Pro and its surprisingly uncommon accessory, the Apple Pencil, I searched in vain for a review that answered my specific questions. The closest I got was this write-up from AnandTech.
But all of that was to be completely expected, because I’m what you call a very narrow use case. I have very peculiar and idiosyncratic desires and interests in a device like the iPad pro. That’s because I’m a mathematics teacher.
I wouldn’t blame you if you aren’t connecting the dots yet. So let me explain. Though this may not be everyone’s memory of it, the fact is that mathematics is a highly visual subject. From the diagrams of deductive geometry, to the construction and interpretation of graphs, to the notation and equations of calculus – understanding and communicating mathematics is saturated with images and symbols. Not only that, the actual thinking and doing of mathematics usually takes place through the medium of this visual language. Mathematicians think by drawing and writing. Drawing and writing aren’t just representations for communicating mathematical thought; they are mechanisms for constructing mathematical thought. That’s why we call it “working out”.
As a mathematics teacher, I do a lot of this mathematical thinking each day. I do it to remind myself of the processes and common misconceptions in what I teach my students; I do it so my students have solutions to the tests I’ve set them; and I do it to answer questions that my students request help with.
What this means is that I end up using a _lot_ of paper. In the course of a normal school year I will produce hundreds of pages of handwritten notes. People tend to give me a bit of a strange look when they see me scrawling marks on a page, partly because I have a reputation (which is, in some ways, justly deserved) for being really into technology and eschewing traditional ways of doing things. (There’s a false dichotomy operating there – I’ll address that in a minute.) “Why don’t you type those notes? Wouldn’t it be better to have all those notes electronically filed and organised?”
The answer, at least to me, is not straightforward. Yes, it’s great having content in an electronic form. It’s easier to search for myself and to share with others. But there’s a price. Computer keyboards were not designed for entering formulas, equations or mathematical notation. Mice were not built with the construction of mathematical diagrams in mind. That’s not their fault; there are hundreds of other tasks that they excel at. Expressing mathematical thought just isn’t one of them. After more than a decade of practice and thousands of hours using a wide range of software platforms that are intended for this purpose, I still find keyboards and mice a wholly inadequate replacement for a simple pencil and paper. When I enter mathematical script using a keyboard, even though I am quite adept at it, my attention is focused on the typing and not the thinking.
An analogy will help here. I grew up in a bilingual home. My parents moved to Australia from Malaysia more than 40 years ago, so they are fluent in English, but it is definitely not the language they are most comfortable with. Despite their preference to speak in Chinese, they made a very deliberate decision to talk to us primarily in English. But because of their background, they experienced significant difficulties with this. I lost count of the number of times they would pause midsentence, frozen in thought, as they translated on-the-fly from their mother tongue into mine. Sometimes they would simply give up, resorting to finishing their sentence in Chinese and leaving me to try and work out their meaning from the context and their body language. And it is the same for me and mathematics. Analogue input is my mother tongue; I can think in it immediately and without interrupting my flow of thought. So while I recognise the importance of having a lot of my mathematics in electronic form (primarily assessment tasks), I have a hard time imagining doing the lion’s share of my mathematical thinking any other way than with a pencil in my hand.
I guess what I’m saying is that I use different technologies constantly and I love the benefit they bring, but I’ve always been very conscious of the (often hidden) disadvantages they include. Failing to do so always leaves us in an exhausting form of technological idealism, where we are constantly looking at the next big app or device as the “thing that will revolutionize education” – and always leaves us disappointed. (The lesson to learn here is that if someone tells you something has a straightforward solution, they are probably trying to sell you something.) That means I reject the notion that we must completely abandon traditional ways of doing things if we are the kinds of people who embrace technology in the classroom.
I’m convinced that there are healthy ways to combine them for the sake of student learning, which is the real goal – not an attitude one way or the other with regard to technology (which is not the heart of the issue). As a result, I always find conversations that are centred on this technology or that technology to be quite dull. I want to talk about the learners and what they are getting out of the different experiences that various platforms or devices can bring. That’s the real currency I deal in.
Which brings me back to the iPad Pro and Apple Pencil. Almost every single detailed review of the Pencil that I’ve found has been focused on its capacity to enable artistic expression. But my primary interest is in the Pencil’s capacity to enable cognitive expression. And without overstating it, after about ten months of non-stop use, I’m ready to deliver my personal verdict.
I love this thing.
I love it because it supports my learning, my explanations, my organisational structures and my thinking. I’ve found it to be so effective that integrating it into my normal workflow has changed the way I do things as fundamentally as the first time I started using email in the cloud or began storing and manipulating data in spreadsheets rather than word processing documents. There’s been a huge shift. Yet while there’s been a massive amount of change, much of what I’ve done has stayed the same – in fact, in some instances, has become more rooted in ways of the past. It’s a living expression of that tension I was talking to you about before. The iPad Pro and Apple Pencil capture that tension in a unique and powerful way that really resonates with me.
So, I’m a fan. But don’t worry, I recognise that these devices are far from perfect – there are some obvious drawbacks that I also want to point out. First, let’s get down to a bit of context which explains the particular way that I use my iPad Pro.
I already own several devices that bear similarities to the Pro. Most obviously, I have an iPad Air 2 that I use for recording my classroom lessons (which I regularly post onto YouTube). Since this iPad has such a specific purpose, for me it overlaps less with the Pro than you would necessarily think; that’s because the Air sits permanently on top of a tripod in the middle of my classroom during my lessons, so I never connect it to my data projector to show visuals or write lesson notes on it. Its next most common use is to edit and upload those videos. When it isn’t occupied for those purposes, the Air does fill the role of a secondary device quite effectively. Like most people, I use it for light email and internet browsing when I’m away from my desk. Because of its size, it’s very handy just to pick up and go when I have to visit a student or teacher quickly then return to my work station; I can use it easily while standing up or walking, which I think is one of the main benefits of tablets in general.
My primary device is a 13.3 inch Windows laptop. I’ve owned laptops up to 15.6 inch before, but found them too bulky and heavy to carry between my classrooms with all the other gear I lug around on a regular basis (textbooks, exam papers, teacher’s diary, pencil case, my iPad Air and the microphone that goes with it). It’s not just my lack of upper body strength that leads me to say that – during my teaching career I’ve used and broken several carry bags, and the point of failure every time is the straps, indicating that I’m always trying to carry too much stuff. For this reason, I’ve also used 10 and 11 inch netbooks before – but I’ve always found them too much of a compromise to use extensively. The lack of a full size keyboard, the diminutive screen that limits my ability to effectively multi-task (e.g. simultaneously viewing my report spreadsheet while writing my reports in a browser) and the inevitably downsized processor/RAM always prevent me from feeling at home on such a small device.
My 13.3 is a very happy compromise between these extremes for me. It’s a Dell XPS 13 that I purchased about two years ago. The screen is a sufficiently high resolution that I can display as much content as I want, and the combination of a high-spec Core i7 processor with loads of RAM and a very handy solid state drive mean that so far it isn’t showing any signs of slowing down. Significantly, the keyboard is a pleasure to use and I can type on it just as fast as I can on any desktop. This is important because it’s the main reason why I decided not to purchase the Smart Keyboard that was designed to pair with the iPad Pro; if I want to do serious typing, I take my laptop. I never intended for the Pro to be a desktop replacement and I wasn’t interested in seeing if it could perform in that role for me.
So then, those are all the ways I _don’t_ use my iPad Pro. What ways _do_ I use it? There are two apps, apart from standard web browsing and email, that dominate my use of the Pro. They are Google Drive (along with its satellite apps, Docs and Sheets) and Notability, which I’ll talk about in turn.
I’ve been into Google Drive for a long time. Back in 2009 I was the intranet coordinator at my school and I drove the school’s adoption of Google Apps for Education. But I would describe myself as having my feet firmly in two camps when it came to using Docs, Sheets and all cloud-based options in general, because while I loved the principle of having everything accessible on all my internet-enabled devices, there were some practical issues that held me back and kept me committed to using desktop software.
The two main issues were formatting and mobile apps. I know it may sound silly, but my time as a semi-professional web, print and graphic designer has really spoiled me in terms of how much control I need over the typography and typesetting in the documents I work with. Things like font face, weight and spacing convey meaning and emphasis. Table layouts and bulleting structure can make the difference between documents that are clear or opaque. Just like a public speaker who has control over their tone, pitch and speed can communicate better than one who does not, software that permits precise control over visual attributes enables us to make documents that are more really digested and understood by readers.
For a long time, Docs and Sheets simply did not give me the amount of freedom I wanted in designing things. But that has improved markedly over the last couple of years, to the point where I can now create a document entirely in Docs and be happy enough with its layout and fonts that I can go directly to print without going anywhere near a desktop program. There are still a few small things in this area where Docs isn’t perfect, the most notable of which is its support for mathematical equations (which is present, but minimal), but I’ve become more and more impressed as years go by and new features are added (for free, I might add!).
The mobile apps are a similar story. I don’t expect an app on a phone or tablet to give me an identical experience to what I’ll get on a desktop in a browser, but got quite a while there was too far a gap between the two. Remembering that the fully-featured versions of Docs and Sheets are kind of like trimmed down versions of their desktop counterparts, and mobile apps are trimmed down versions of their browser counterparts, you can see that if you were on an iPad you were getting a very lightweight experience of spreadsheets and word processing. But recently, the native iOS apps for Docs, Sheets and Drive have gained a core feature set that makes them genuinely useful and sometimes even a pleasure to work with. More and more, I’ve found myself able to do everything I need on my tablet while in my classroom without needing to return to my desk – it’s been liberating.
That brings me to Notability. As I said earlier, I had a very clear use for my iPad Pro in mind from the beginning, so one of the very first things I did during my initial setup of the Pro was to download every note-taking app I could find. Trawling the internet for reviews and soliciting some of my online contacts for suggestions, I settled on the following list of apps to try:
- Notes (i.e. the default iOS app)
- Penultimate
- OneNote
- Upad
- Notability
There are two apps that I installed but did not include on that list – Explain Everything and Doceri. Both of these are screencasting apps, which I was interested in at a basic level, but as I’ve stated above, was not my main intention for the Pro. Neither app is updated for the Pro’s higher resolution yet, so I haven’t invested any time to really give either of them a proper try.
The five apps on my list are, by contrast, note-taking apps through and through. I used each one extensively for about a week before moving onto the next one, so that I could gain a deep sense of each app’s strengths and shortcomings. So here’s my app-by-app overview:
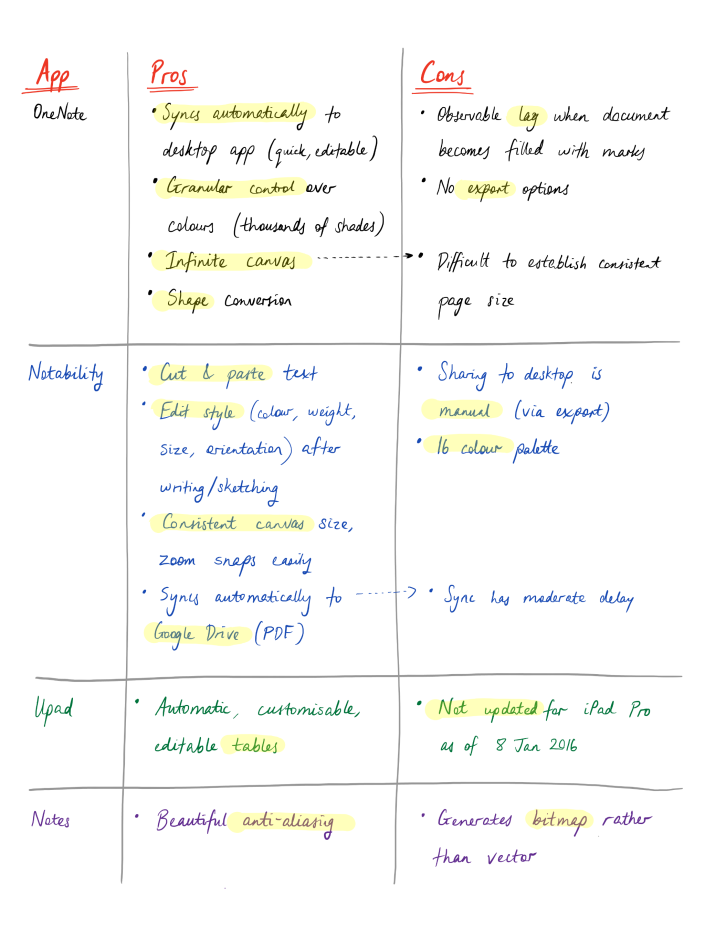
Notability came out as the clear front-runner. Probably the two most distinctive and frequently useful features were (1) its ability to modify text/diagrams after they are written/drawn and (2) its seamless integration with Google Drive, which makes the content I create in Notability instantly more shareable and useful. (From the PDF I can print in high quality since it exports my writing as vectors rather than bitmaps, or I can just email it to someone if that is more convenient. I’ve done both of these several times at work over the last three months and have been very pleased with the output.)

I do want to say something about my overall writing experience across all apps – in other words, what I found to be true because of the way Apple has designed the Pro and the Pencil. Essentially, it feels like magic. After about 2 months of daily use, I reached the point where it felt equally natural to write on the Pro as I did on paper. I no longer notice things like the smoothness of the glass and the Pencil itself, which I remember bothering me at the beginning. In fact, I even find it easier to write with the Pencil over long periods of time because I only have to apply minimal pressure to make clear marks (when I write on paper, out of habit I press quite hard with my pen).
These have been said many times before, so I won’t dwell on them: the lack of discernible lag and the highly reliable palm rejection are the main things that make the Pencil feel so compelling in normal use. My handwriting on the Pro looks exactly my handwriting on paper, and that’s because Apple has successfully engineered the Pencil and Pro so that you don’t need to adjust the way you write to use them effectively.
And this is what makes the whole experience so effective for me as a mathematics teacher. Essentially the Pro has taken all the handwriting I would normally be doing – and as I’ve established, that’s a lot – and supercharged it by integrating it into an electronic workflow. I have several “subjects” set up in Notability, each of which syncs automatically to a separate folder in Google Drive. The synchronisation happens seamlessly in the background whenever I close a document – which means I don’t have the live version backed up like I do in Google Docs or Microsoft OneNote, but if I want to manually trigger the app to update a file on Drive then all I have to do is close and re-open it. This means that whenever I need a document, no matter how long ago I’ve made it, I can get to it from any of my internet-connected devices. This has been useful on dozens of occasions already – taking minutes on a meeting and immediately emailing them out to staff, pulling up an example worked solution to a question posed by a student about a topic we’d looked at several weeks prior, and displaying the solutions to a past exam paper (along with my live annotations) on a data projector for the whole class to see, among many other examples of how this has been useful to me.

One feature that I particularly want to highlight is the ability to select and rearrange or cut and paste marks on the page. I want to point it out because it’s a feature I didn’t even know I wanted – but once I understood it and got used to it, found myself using it constantly (literally, hundreds of times a day) and really miss being able to do it when I return to writing on paper. This takes one of the very best features of typing and imports it into the sphere of handwriting. Anyone who writes frequently – whether it’s emails, essays, reports, articles or fiction – basically takes it for granted that we write (and think) in stops and starts. It’s rare to find someone who can think of the perfect words and grammar to convey their meaning in the exact order and at the exact speed to type them down. Most of us need to write, delete, rephrase, and edit several times before we get something we’re satisfied with. Personally, I tend to write/type out my ideas and then read my sentences back to myself as if I were speaking them to get a sense as to whether a sentence is clear or not. I like to ensure that my paragraphs have a measure of rhythm to them, and this usually requires copious editing.
Proofreading sentences (and equations!) is equally easy on a hard copy as it is on a digital copy. But the actual act of reworking something so that it’s clearer or more powerful is immensely easier to do on a computer. The ease with which you can rearrange and replace phrases (or mathematical symbols) is one of the killer features on a digital word processor, something that we often take for granted when all we do is type all day. And being able to do that with the handwritten script I produce through the Pencil is truly like having the best of both worlds.
Here, at the end of this article, let me mention something which is usually the first thing you find in a review about the iPad Pro: its size. Putting together this write-up has taken me such a long time that Apple has already released its “next” version of the iPad Pro – the 9.7 inch version (i.e. in the same form factor as the iPad Air). However, given my time to settling into using the original Pro, I think 12.9 inches is the best size for this device.
Let me take a step back before I justify that opinion. Okay, I get it: everyone is gobsmacked by the Pro’s size when they first see it. It’s always the first thing people comment on when they see me using it. That’s unsurprising for two reasons: (1) the Pro’s size is the only fact about it you can notice within 1 second of seeing it, and (2) everyone is mentally comparing the Pro to a 9.7 inch tablet, because that’s what they’re used to. The first point is obviously unavoidable, but I think the second point is actually an honest mistake. I don’t think the Pro is trying to be a better version of the Air; I think it’s trying to be something else altogether (hence the Pro moniker). If you’ve read this far into this post turn you probably won’t be surprised when I say I think the Pro is just the right size at 12.9 inches because of what I am comparing it to: an A4 piece of paper. The writable surface of each is basically identical, and I don’t want either of them to be any smaller than they are right now.
There are other benefits, too. I’ve tried doing Split Screen on a 9.7 inch screen and it feels just like it did on those 10 inch netbooks I mentioned earlier: cramped and not designed for this purpose. But I’ve done legitimate multi-tasking on the Pro numerous times and found it quite a comfortable experience (most frequently with Notability on the left and iBooks, email or Safari on the right).
So, here ends my rambling set of thoughts on the iPad Pro and Apple Pencil. I felt compelled to write about them because they are that rare instance of technology that has genuinely managed to make me adjust my workflow because I get access to significant new benefits this way. There are lots of things I haven’t said but I’ve already written far too much here – so I hope it’s helpful to some of you and if you’ve got further questions, feel free to send them my way!








